力扣 704

  二分查找
  这道题目可以用暴力解法，也就是遍历数组元素，但是这样做的时间复杂度是 $\small {O (N)}$。因此可以采取二分法对题目进行求解。设定开始查找的范围为 [left, right]，比较区间中点 mid 的值和 target 的大小，如果小于 target 说明 target 在 [mid + 1, right] 之间，如果大于 target 说明 target 在 [left, mid - 1] 之间。每轮根据区间修改 left 或 right 的值，如果 left > right，说明数组中没有 target 目标值，返回 - 1。知道了二分法的原理，编写下面的代码：

int search(vector<int>& nums, int target)
{
    int left = 0;
    int right = nums.size() - 1;
    while(left <= right)
    {
        int mid = (right - left) / 2 + left;
        int num = nums[mid];
        if(num == target)
        {
            return mid;
        }
        else if(num > target)
        {
            right = mid - 1;
        }
        else left = mid + 1;
    }
    return -1;
}

  时间复杂度为 $\small {O (\mathrm {log}(N))}$。

力扣 27

  移除元素
  这个题目可以用双指针的方法进行解答。假定现在有两个指针，一个叫 slow，一个叫 fast，他们起始都指向数组 nums 的第一个元素 nums [0]，然后判定 nums [fast] 是否与 val 相等，如果相等，fast++，如果不相等就把 nums [fast] 的值给 nums [slow]，fast++，slow++。可以看到，这个操作实际上就是将非 val 的元素向前挪动，覆盖掉值为 val 的元素。这样无论 nums 数组后的元素是什么，只要保证返回的前 k 个元素不包含 val 就行。因此循环判定的条件就是 fast < nums.size()。代码编写如下：

int removeElement(vector<int>& nums, int val)
{
    int slow = 0, fast = 0;
    while(fast < nums.size())
    {
        if(nums[fast] != val)
        {
            nums[slow++] = nums[fast++];
        }
        else fast++;
    }
    return slow;
}

  时间复杂度为 $\small {O (N)}$，空间复杂度为 $\small {O (1)}$。

力扣 977

  有序数组的平方（双指针）
  这个题可以直接先平方后 sort 排序的方法，但是这样做的时间复杂度为 $\small {O (n\mathrm {log} n)}$，空间复杂度为 $\small {O (\mathrm {log} n)}$。代码如下：

vector<int> sortedSquares(vector<int>& nums)
{
    for(int i = 0; i < nums.size(); i++)
    {
        nums[i] *= nums[i];
    }
    sort(nums.begin(), nums.end());
    return nums;
}

  其实也可以采用双指针的办法。题目告诉了数组是有序的，那么设定指针 left 和指针 right，并新建一个数组 res，大小和 nums 一样。left 指向 nums 第一个元素，right 指向 nums 的最后一个元素。如果 nums [left]^2 > nums [right]^2，那么就把 left 的运算结果给 res 最右侧未被赋值的元素 k，此时 left++，k- -。同理，当 nums [left]^2 < nums [right]^2 ，那么就把 right 的运算结果给 res 最右侧并 right- -，k- -。以此类推。

vector<int> sortedSquares(vector<int>& nums)
{
    vector<int> res(nums.size(), 0);
    int k = nums.size();
    int left = 0, right = nums.size() - 1;
    while(left <= right)
    {
        if(nums[left] * nums[left] <= nums[right] * nums[right])
        {
            res[k--] = nums[right] * nums[right];
            right--;
        }
        else
        {
            res[k--] = nums[left] * nums[left];
            left++;
        }
    }
    return res;
}

  时间复杂度为 $\small {O (n)}$，空间复杂度为 $\small {O (1)}$。

力扣 209

  长度最小的子数组（双指针）
  这个题目可以用滑窗思想进行求解，仍然可以采用双指针，一个起始指针 i 和末尾指针 j，以示例 1 为例。开始 i 和 j 都指向 nums [0]，然后 j++，统计 i 和 j 之间元素和 sum。当 j = 3 时，sum = 8 > 7，此时长度为 res = 4。为了找到最小的长度，令 i++，sum = 6，不符合要求。此时 j++，开启下一轮的查找。此时 sum = 10，res = 4，令 i++，sum = 7，res = 3；i++，sum = 6，不符合要求…… 以此类推，直到当 i = 5，j = 6，sum = 7，res = 2。得到最后结果。代码实现如下：

int minSubArrayLen(int target, vector<int>& nums)
{
    int res = INT32_MAX;//设置窗口最大值，以方便比较
    int i = 0;
    int sum = 0;
    int windsize = 0;
    for(int j = 0; j < nums.size(); j++>)
    {
        sum += nums[j];
        while(sum >= target)
        {
            windsize = j - i + 1;
            res = res > windsize ? windsize : res;
            sum -= nums[i++];
        }
    }
    return res == INT32_MAX ? 0 : res;
}

力扣 59

  螺旋矩阵 Ⅱ
  这个题的难点在于如何编程实现螺旋顺序的矩阵元素访问。这里假设矩阵的四个顶点分别为 left_Top (Lt)、left_Bottom (Lb)、Right_Top (Rt)、Right_Bottom (Rb)，并将他们的值设置为：

int Lt = 0;
int Lb = n - 1;
int Rt = 0;
int Rb = n - 1;

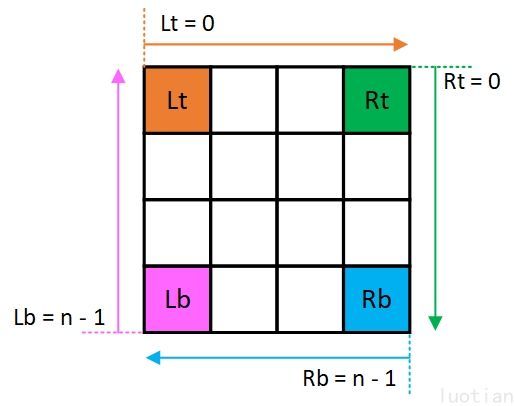
  设定 Lt 方向为 → ， Rt ↓ ， Rb ← ， Lb ↑ 。这里四个顶点的坐标并不重要，重要的是这四个顶点标明了矩阵的旋转方向和坐标边界值。下面对坐标边界值进行说明。
  设定 Lt 和 Rb 是两个相对方向，那么列方向上坐标边界值就是 Lt = 0 和 Rb = n - 1。同理，Lb 和 Rt 是另外两个相对的方向，行方向上坐标边界值就是 Rt = 0，Lb = n - 1。
  知道了这些条件，现在加入一个变量 i：

  1. 起始时 Lt → Rb（虽然实际上是 Lt → Rt，但 Lt 和 Rb 是左右两个相对方向），矩阵遍历下标为 [Rt][i]，因为这里相当于是 “ 行 = Rt = 0 ” 是定值，“列 = i = Lt → Rb ” 是变值。当列遍历完成，Rt++，相当于第 0 行现在已经填充好了元素，因此 Rt 需要向下移动一行。
  2. 第二步 Rt → Lb（虽然实际上是 Rt → Rb，但 Rt 和 Lb 是上下两个相对方向），矩阵遍历下标为 [i][Rb]，因为这里相当于是 “ 列 = Rb = n - 1 ” 是定值，“行 = i = Rt → Lb ” 是变值。当列遍历完成，Rb- -，相当于第 n - 1 列现在已经填充好了元素，因此 Rb 需要向左移动一行。
  3. 第三步 Rb → Lt，[Lb][i]，Lb- -。
  4. 第四步 Lb → Rt，[i][Lt]，Lt++。
  5. 当矩阵填充值大于 $\small {n \times n}$ 说明已经填充完毕，退出循环。

  通过上述步骤就实现了矩阵的螺旋顺序访问。这个原理不仅可以用于顺时针，还可以用于逆时针。

vector<vector<int>> generateMatrix(int n)
{
    vector<vector<int>> res(n, vector<int>(n));
    int Lt = 0, Lb = n - 1, Rt = 0, Rb = n - 1;
    int count = 1;
    int flag = n * n;
    while(count <= flag)
    {
        for(int i = Lt; i <= Rb; i++)
        {
            res[Rt][i] = count++;
        }
        Rt++;
        for(int i = Rt; i <= Lb; i++)
        {
            res[i][Rb] = count++;
        }
        Rb--;
        for(int i = Rb; i >= Lt; i--)
        {
            res[Lb][i] = count++;
        }
        Lb--;
        for(int i = Lb; i >= Rt; i--)
        {
            res[i][Lt] = count++;
        }
        Lt++;
    }
    return res;
}