力扣刷题 - 链表

  对于一个链表，C++ 的定义如下：

struct ListNode {
    int val;
    ListNode *next;
    ListNode() : val(0), next(nullptr) {}
    ListNode(int x) : val(x), next(nullptr) {}
    ListNode(int x, ListNode *next) : val(x), next(next) {}
};

  链表结构可由下表征：

力扣 203

  移除链表元素
  这个题由于涉及到头节点的变动，因此可以先设置一个空的前置节点 dummy，然后将 dummy 指向 head。为了对 dummy 的指针指向进行保留，这里复制一个指针 temp = dummy。接下来是两种情况，当 temp->next->val == val，那么 temp->next = temp->next->next。否则 temp 指针移动，temp = temp->next。

ListNode* removeElements(ListNode* head, int val)
{
    struct ListNode* dummy = new ListNode(0, head);
    struct ListNode* temp = dummy;
    while(temp->next != NULL)
    {
        if(temp->next->val == val)
        {
            temp->next = temp->next->next;
        }
        else
        {
            temp = temp->next;
        }
    }
    return dummy->next;
}

时间复杂度为 $\small {O (n)}$，空间复杂度为 $\small {O (1)}$。

力扣 707

  设计链表

class MyLinkedList {
public:
    // 初始化链表，大小为 0 ，头结点的值为 0
    // this指针用于访问类的成员变量和成员函数
    MyLinkedList() {
        this->head = new ListNode(0);
        this->size = 0;
    }
    // 获得指定节点的值
    int get(int index) {
        // 这里 >= size 是因为元节点的下标是 0，末尾节点的下标是 size - 1
        if (index < 0 || index >= size) {
            return -1;
        }
        // 定义一个指针 cur 指向头结点，这样不会改变head中的值
        ListNode* cur = head;
        // 遍历链表，直到遍历下标为 index 的节点
        for (int i = 0; i <= index; i++)
        {
            cur = cur->next;
        }
        return cur->val;
    }
    // 在 0 位置添加节点，就相当于在头部添加节点
    void addAtHead(int val) {
        addAtIndex(0, val);
    }
    // 在 size 位置添加节点，就相当于在末尾添加节点
    void addAtTail(int val) {
        addAtIndex(size, val);
    }
    // 在index处添加节点
    void addAtIndex(int index, int val) {
        // 如果 index 大于 size，则不添加节点
        if (index > size)
            return;
        // 如果 index 小于 0，则将 index 置为 0
        index = max(0, index);
        // 添加节点，size++
        size++;
        ListNode* temp = head;
        // 定位到 index 前一个节点
        for (int i = 0; i < index; i++)
        {
            temp = temp->next;
        }
        // 添加新的节点
        ListNode* NewNode = new ListNode(val);
        // 插入新的节点
        NewNode->next = temp->next;
        temp->next = NewNode;
    }
    void deleteAtIndex(int index) {
        //这里取 >= 是因为元节点下标是 0
        if (index < 0 || index >= size)
            return;
        size--;
        ListNode* temp = head;
        for (int i = 0; i < index; i++)
        {
            temp = temp->next;
        }
        ListNode* p = temp->next;
        temp->next = temp->next->next;
        // 释放被删除节点的内存
        delete p;
    }
private:
    struct ListNode {
        int val;
        ListNode* next;
        ListNode() : val(0), next(nullptr) {}
        ListNode(int x) : val(x), next(nullptr) {}
        ListNode(int x, ListNode* next) : val(x), next(next) {}
    };
    int size;
    ListNode* head;
};

力扣 206

  反转链表
  这个题可以用双指针的解法。设定慢指针 slow = NULL，快指针 fast = head。现在开始遍历。设置 temp = fast->head，保存 fast 的下一个节点。这里为了反转链表，需要将 fast->next 指向上一个节点 slow，因此有 fast->next = slow。现在反转了链表。开始移动 fast 和 slow 指针。这里先移动 slow 指针，由于现在 slow 已经完成任务，slow 需要向右移动一位，也就是 slow = fast。然后 fast 也向右移动一位，也就是 fast = temp。这一轮的反转就完成了。
  由于 fast 比 slow 快一格，而题目要求要返回反转后的头节点，所以 fast 要遍历到原链表的 NULL 处。

ListNode* reverseList(ListNode* head)
{
    ListNode* slow = NULL;
    ListNode* fast = head;
    while(fast != NULL)
    {
        ListNode* temp = fast->next;
        fast->next = slow;
        slow = fast;
        fast = temp;
    }
    return slow;
}

力扣 24

  两两交换链表中的节点
  这个题说了两两交换，那么只研究前两个节点之间的连接关系就行。为了让节点访问更方便，还是要在链表前插入一个虚拟头节点 dummy。那么对于 dummy 和 node1 和 node2，两两交换就是将节点 dummy->node1->node2 变成 dummy->node2->node1，其他两两节点可依此类推。设定节点 temp = dummy，想完成交换，首先让 temp -> node2，然后 node1 -> node3，最后 node2 -> node1。然后更新 temp 向右移动两个节点，也就是 temp = node1（此时 node1 已经成为了链表中第二个节点），开始下一轮循环。循环的终止条件需要注意，要把 temp->next != NULL 放在前面，不然如果 temp->next == NULL，temp->next->next 就是非法访问，会编译出错。

ListNode* swapPairs(ListNode* head)
{
    // 节点 0
    ListNode* dummy = new ListNode(0, head);
    ListNode* temp = dummy;
    // 第一个说明当链表是偶数个节点，第二个说明当链表是奇数个节点
    while(temp->next != NULL && temp->next->next != NULL)
    {
        //节点 1
        ListNode* node1 = temp->next;
        //节点 2
        ListNode* node2 = temp->next->next;
        //节点 dummy -> 节点 2
        temp->next = node2;
        //节点 1 -> 节点 3
        node1->next = node2->next;
        //节点 2 -> 节点 1
        node2->next = node1;
        //节点 temp = 节点 1 （步进两个节点）
        temp = node1;
    }
    ListNode* res = dummy->next;
    delete dummy;
    return res;
}

力扣 19

  删除链表倒数第 N 个节点
  这个题乍一看需要遍历两遍链表，第一遍遍历得到链表的大小，第二遍遍历得到需要删除的元素的位置。不过可以换个思路，将两个遍历合并成一个。这里需要用到双指针的策略。首先定义 fast 和 slow 指针，刚开始先移动 fast 指针，让 fast 和 slow 的距离为 n 个节点。然后开始同步移动 fast 和 slow，当 fast 的下一位是 NULL 时，此时 slow 的下一位就是要删除的节点，这个时候就只需要 slow->next = slow->next->next 即可删除节点。

ListNode* removeNthFromEnd(ListNode* head, int n)
{
    // 定义快慢指针
    ListNode* fast = new ListNode(0, head);
    ListNode* slow = fast;
    // 定义临时头节点
    ListNode* dummy = fast;
    // 如果 n <= 0 无效
    if(n <= 0)
    {
        return dummy->next;
    }
    // 开始移动 fast 指针，当移动 n 步后停止
    for(int count = 1; count <= n; count++)
    {
        if(fast->next != NULL)
        {
            fast = fast->next;
        }
        // 如果 fast 下一位为空但是遍历次数还没达到 n 次说明 n 的大小超过链表大小，访问无效
        else if(count < n)
        {
            return slow->next;
        }
    }
    // 开始同步移动 fast 和 slow，如果 fast 的下一位为 NULL，说明到了链表末尾。此时 slow 的下一位就是要删除的节点
    while(fast->next != NULL)
    {
        fast = fast->next;
        slow = slow->next;
    }
    // 删除节点
    ListNode* temp = slow->next;
    slow->next = slow->next->next;
    delete temp;
    // 返回链表头节点
    return dummy->next;
}

  时间复杂度为 $\small {O (L)}$，$\small {L}$ 为链表长度。空间复杂度为 $\small {O (1)}$。

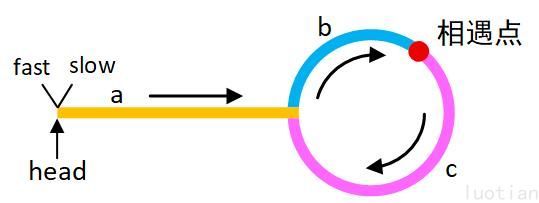
力扣 142

  环形链表 Ⅱ
  判断链表中有没有环，可以近似成操场跑圈的相遇问题。假设有两个人同时起跑，一个人快，一个人慢，那么经过一段时间，他们一定可以在操场上的某个位置相遇。那么对于这个题目，定义一个快指针 fast 和一个慢指针 slow ，慢指针每次移动一格，快指针每次移动两格，如果链表存在环，他们必定会在环中相遇，如果链表不存在环，他们不可能相遇。
  解决了链表中是否有环的问题，接下来解决如何找到环的入口。定义进入环之前的路程为 $\small {a}$，slow 进入环后走了 $\small {b}$ 路程和 fast 相遇，环的路程为 $\small {b + c}$，那么可以得知在 slow 进入环前 fast 已经在环内行走了 $\small {n (b + c)}$ 的路程，其中有 $\small {n\geqslant 1,n\in \mathbf {N}_+}$。根据上面的条件，列出等式：
$$a+b=\frac{a+n\left( b+c \right) +b}{2}$$
  化简后得：
$$a=\left( n-1 \right) \left( b+c \right) +c$$
  这表明 slow 走过 $\small {n-1}$ 个完整的环后，再走过路程 $\small {c}$ 必定和路程 $\small {a}$ 相等。因此定义一个新的指针 index = head，index 和 slow 每次步进 1 个节点，那么相遇的节点就是环的入口。

ListNode *detectCycle(ListNode *head)
{
    ListNode* fast = new ListNode(0, head);
    ListNode* slow = fast;
    // 这里要确保fast接下来的两个节点都不为空
    while(fast->next != NULL && fast->next->next != NULL)
    {
        // 这里要先进行指针移动，否则初始条件下 fast == slow 会出问题
        fast = fast->next->next;
        slow = slow->next;
        if(fast->next == slow->next)
        {
            ListNode* index = head;
            slow = slow->next;
            while(index != slow)
            {
                index = index->next;
                slow = slow->next;
            }
            return index;
        }
    }
    // 链表没有环，返回空指针
    return nullptr;
}

力扣 15

  三数之和
  这个题用哈希表做会变得非常麻烦，还是得用双指针的方法。设定 i、left、right 分别对应三个数的元素下标，取值为：

int i = 0; i < nums.size();
int left = i + 1;
int right = nums.size() - 1;

  这里没有说返回的数组是有序的，那么可以先对数组从小到大进行排序，然后再遍历数组，这样做是因为三数相加为 0，也就是 $\small {a + b+c = 0}$，$\small {a\leqslant b\leqslant c}$。那么一定有 $\small {a\leqslant 0}$，因此有了第一个判断条件，如果 nums [i] > 0，直接返回结果，不用再遍历了。
  然后对 $\small {a}$ 进行去重，为了说明去重的必要性，举例 [-1, -1, -1, 0, 1]，可以看到结果是 [-1, 0, 1]，但是 - 1 会有多个不同的取值。在这里就需要判断，如果当 i 元素和 i - 1 元素值相同，那么就跳过此轮遍历。
  然后添加 while 循环，判断三数之和是否为 0，如果大于 0，说明 nums [right] 太大了，将 right- -，如果小于 0，说明 nums [left] 太小了，将 left++。如果三数之和等于 0，那么就保存 i、left、right 对应元素值。
  这个时候我们还要注意，如果有这样的情况 [-1, -1, 0, 0, 1, 1]，多个 left 和 right 满足要求，就需要对 left 和 right 进行去重。在等于 0 的判断下，添加 while 循环，当 right 和 right - 1 元素相等，right- -，当 left 和 left + 1 元素相等，left++。这里注意无论是否进入去重的 while 循环，最后都要更新 right 和 left。
  所有 while 循环都要加上 right > left 条件防止出错。

vector<vector<int>> threeSum(vector<int>& nums)
{
    vector<vector<int>> res;
    sort(nums.begin(), nums.end());
    for(int i = 0; i < nums.size(); i++)
    {
        if(nums[i] > 0)
            return res;
        if(i > 0 && nums[i] == nums[i - 1])
            continue;
        int left = i + 1;
        int right = nums.size() - 1;
        while(right > left)
        {
            if(nums[i] + nums[left] + nums[right] > 0) right--;
            else if(nums[i] + nums[left] + nums[right] < 0) left++;
            else
            {
                res.push_back(vector<int>{nums[i], nums[left], nums[right]});
                while(right > left && nums[right] == nums[right - 1]) right--;
                while(right > left && nums[left] == nums[left + 1]) left++;
                right--;
                left++;
            }
        }
    }
    return res;
}

时间复杂度是 $\small {O (N^2)}$。

力扣 18

  四数之和
  这个题目和三数之和原理一致，也是使用双指针的方法，不过由于这个题目是 4 数相加，而且 target 是任意值，在去重方面还是有些不一致。

vector<vector<int>> fourSum(vector<int>& nums, int target)
{
    vector<vector<int>> res;
    sort(nums.begin(), nums.end());
    for(int k = 0; k < nums.size(); k++)
    {
        // 第一次剪枝
        if(nums[k] > target && (nums[k] >= 0 || target >= 0))
            break;// 终止循环
        // 对 k 去重，原理和上一题 i 去重一样
        if(k > 0 && nums[k] == nums[k - 1]) continue;
        for(int i = k + 1; i < nums.size(); i++)
        {
            // 第二次剪枝
            // 如果前两数大于 target，且 nums[i] 大于 0，后面的数再加一定大于零，直接终止循环
            if(nums[k] + nums[i] > target && nums[i] >= 0) break;
            // 对 i 去重，原理和上一题 i 去重一样
            if(nums[i] == nums[i - 1] && i > k + 1) continue;
            // 下面代码逻辑不变
            int left = i + 1;
            int right = nums.size() - 1;
            while(right > left)
            {
                // 要转成long，不然会溢出
                if((long)nums[k] + nums[i] + nums[left] + nums[right] > target) right--;
                else if((long)nums[k] + nums[i] + nums[left] + nums[right] < target) left++;
                else
                {
                    res.push_back(vector<int>{nums[k], nums[i], nums[left], nums[right]});
                    while(right > left && nums[right] == nums[right - 1]) right--;
                    while(right > left && nums[left] == nums[left + 1]) left++;
                    right--;
                    left++;
                }
            }
        }
    }
    return res;
}