西电通院信号与系统大作业 — 无线传输
一、题目描述
考虑一个余弦信号 $\small {x\left (t \right) =\cos \left (2\pi f_0t \right)}$ 沿着一条受到多径效应和多普勒效应影响的信道传输的情形。设有两条路径,并且假定该正弦信号正由一个移动的物体发出,因此会发生多普勒频移。设接收信号为:
$$
\begin{aligned}
r\left( t \right) =a_0\cos\left( 2\pi \left( f_0-v \right) \left( t-\dfrac{L_0}{c} \right) \right) +a_1\cos\left( 2\pi \left( f_0-v \right) \left( t-\dfrac{L_1}{c} \right) \right)
\end{aligned}
$$
其中 $\small {0\le a_i\le 1,i = 0,1}$ 为衰减因子,$\small {L_i}$ 代表第 $\small {i}$ 条路径上发射机与接收机之间的距离,$\small {c = 3\times 10^3m / s}$,$\small {v}$ 是多普勒效应引起的频移。
二、问题回答
设 $\small {r_0 (t)}$ 和 $\small {r_1 (t)}$ 分别为两条信号路径分量,即:
$$r_0(t) = a_0\cos\left[2\pi\left(f_0-v\right)\left(t-\frac{L_0}{c}\right)\right]$$
$$r_1(t) = a_1\cos\left[2\pi\left(f_0-v\right)\left(t-\frac{L_1}{c}\right)\right]
$$
2.1 问题 1
令 $\small {f_0 = 2 \mathrm {kHz}, v = 50\mathrm {Hz}, a_0 = 1, a_1 = 0.9}$。令 $\small {L_0 = 10000 m}$,如果两个余弦信号的相位差等于 $\small {\pi / 2}$,$\small {L_1}$ 应该等于多少?
答:
上述数据带入 $\small {r_0 (t)}$ 和 $\small {r_1 (t)}$ 中得:
$$\varphi_0 = -13000\pi$$
$$\varphi_1 = -\frac{13}{10}\pi L_1$$
由于 $\small {\Delta\varphi=\left (2n+\frac {1}{2}\right)\pi}$,因此:
$$13000\pi - \frac{13}{10}\pi L_1 = \left(2n+\frac{1}{2}\right)\pi, \quad n\in \mathbf{Z}$$
解得:
$$L_1 = \frac{129995}{13} - \frac{20}{13}n, \quad n\in \mathbf{Z}$$
当 $\small {n = 0}$ 时,$\small {L_1=\frac {129995}{13} m \approx 9999.62 m}$。
2.2 问题 2
若各参数同上,但 $\small {L_1 = 10000 m}$,那么接收信号 $\small {r (t)}$ 是周期的吗?如果 $\small {r (t)}$ 是周期的,那么它的周期等于多少?它的周期与原始余弦信号的周期相差多少?如果将传输信道看作为一个系统,$\small {x (t)}$ 是其输入,$\small {r (t)}$ 是其输出,那么该系统是线性的和时不变的吗?请作出解释。
答:
将所给数据代入 $\small {r (t)}$ 中得:
$$r(t) = 1.9\cos(3900\pi t - 13000\pi)$$
可以发现 $\small {r (t)}$ 是周期信号,其周期 $\small {T=\frac {2\pi}{\omega} \approx 5.13 \times 10^{-4} s}$。
将数据代入得:
$$x(t)=\cos(4000\pi t)$$
可知周期 $\small {T_x = 5 \times 10^{-4} s}$,因此二者周期差为:
$$\Delta T = \frac{1}{78000} s \approx 1.28 \times 10^{-5} s$$
下面判断该系统是否为线性系统,是否为时不变系统。
根据 $\small {r (t)}$ 和 $\small {x (t)}$ 的解析式可以得出二者满足以下关系:
$$r\left( t \right) =1.9x\left( \frac{39}{40}t \right) $$
-
线性系统的判断
对假设两个输入 $\small {x_1 (t), x_2 (t)}$ 分别对应输出 $\small {r_1 (t), r_2 (t)}$,即:
$$r_1(t) = 1.9 x_1\left(\frac{39}{40}t\right)$$
$$r_2(t) = 1.9 x_2\left(\frac{39}{40}t\right)$$
当输入为 $\small {ax_1 (t) + bx_2 (t)}$ 时,输出为:$$
\begin{aligned}
r(t) &= 1.9a x_1\left(\frac{39}{40}t\right) + 1.9b x_2\left(\frac{39}{40}t\right)
\end{aligned}
$$因此该系统是线性的。
-
时不变系统的判断:
对输入 $\small {x (t)}$ 有:
$$r\left( t \right) =1.9x\left( \frac{39}{40}t \right) $$
令输入产生 $\small {t_d}$ 的时移即 $\small {x (t-t_d)}$,有:$$ r’\left( t \right) =1.9x\left( \frac{39}{40}t-t_d \right) $$
$$r(t-t_d) = 1.9 x\left(\frac{39}{40}(t-t_d)\right) = 1.9 x\left(\frac{39}{40}t - \frac{39}{40}t_d\right)$$
显然有:
$$r’(t) \neq r(t-t_d)$$
系统为时变系统。
2.3 问题 3
对信号 $\small {x (t)}$ 和 $\small {r (t)}$ 以抽样频率 $ \small {F_s = 10\mathrm {kHz
}}$ 进行抽样,画出抽样后的发送信号 $\small {x (n T_s)}$ 和接收信号 $\small {r (n T_s)}$ 的图形,取 $\small {n = 0\sim 2000}$。
答:
-
对 $\small {x (t)}$ 进行采样:
原始余弦信号 $\small {x\left (t \right) =\cos \left (2\pi f_0t \right)}$。以抽样频率 $\small {F_s = 10\mathrm {kHz}}$ 进行取样,则取样周期 $\small {T_s = 10^{-4} s}$,取样函数为:
$$s\left( t \right) =\sum_{n=-\infty}^{+\infty}{\delta \left( t-10^{-4}n \right)}$$
则取样信号:
$$x_s\left( t \right) =\cos \left( 2\pi f_0t \right) \sum_{n=-\infty}^{+\infty}{\delta \left( t-10^{-4}n \right)}$$由于不同的 $\small {f_0}$ 在抽样频率一定的情况下会对 $\small {x (nT_s)}$ 产生不同的结果,因此取 $\small {f_0 = 2\mathrm {kHz},7\mathrm {kHz}}$,采用 MATLAB 进行仿真,结果如图所示:
$\small {f_0 = 2\mathrm {kHz}}$ 下的 $\small {x (t)}$ 抽样结果图 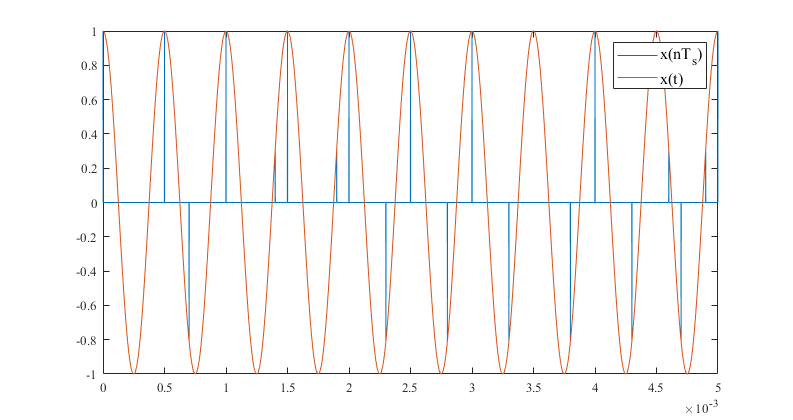
$\small {f_0 = 7\mathrm {kHz}}$ 下的 $\small {x (t)}$ 抽样结果图 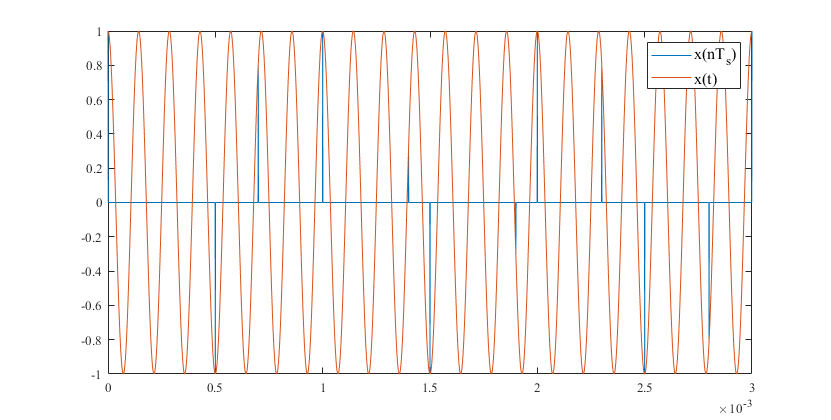
由图可以发现,信号频率为 $\small { 2\mathrm {kHz}} $ 时,抽样图形很明显地呈现了原始信号的特征,而信号频率为 $\small { 7\mathrm {kHz}} $ 时,在采样信号的过程中出现了信号混叠的现象。这是因为采样允许的最小频率至少应为原信号最高频率的两倍,该频率称为奈奎斯特频率。当取样的信号频率为 $\small { 2\mathrm {kHz}} $ 时,奈奎斯特频率为 $\small { 4\mathrm {kHz}} $,$\small { F_s = 10\mathrm {kHz}} $ 符合采样要求;当取样的信号频率为 $\small { 7\mathrm {kHz}} $ 时,$\small {F_s} $ 将不符合采样要求。因此,选择的信号频率应当低于 $\small { 5\mathrm {kHz} }$。
-
对 $\small {r (t)}$ 进行采样:
接收信号 $\small {r (t)}$,以抽样频率 $\small { F_s = 10\mathrm {kHz} }$ 进行取样,则取样周期 $\small { T_s = 10^{-4} s}$,取样函数为:
$$s\left( t \right) =\sum_{n=-\infty}^{+\infty}{\delta \left( t-10^{-4}n \right)}$$
则取样信号:
$$r_s\left( t \right) =\mathrm{r(}t)\sum_{n=-\infty}^{+\infty}{\delta \left( t-10^{-4}n \right)}$$
选取信号频率 $\small { f_0 = 2\mathrm {kHz}}$,其余条件同问题 2,则:
$$r_s\left( t \right) =1.9\cos\left( 3900\pi t-13000\pi \right) \sum_{n=-\infty}^{+\infty}{\delta \left( t-10^{-4}n \right)}$$
采用 MATLAB 进行仿真,结果如图所示:
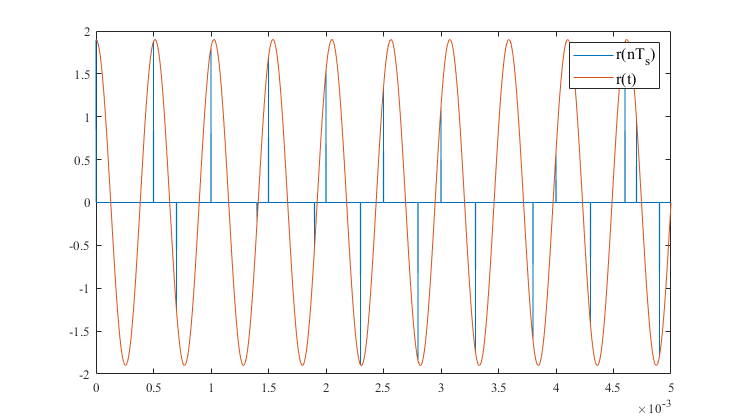
2.4 问题 4
考虑这样一种情形,其中 $\small {f_0 = 2\mathrm {kHz}}$,但路径参数是随机的。尝试模拟一种真实情形,其中路径参数都是不可预测的(虽然它们之间仍存在某种关系)。令
$$r\left( t \right) =a_0\cos\left( 2\pi \left( f_0-v \right) \left( t-\frac{L_0}{c} \right) \right) +a_1\cos\left( 2\pi \left( f_0-v \right) \left( t-\frac{L_1}{c} \right) \right) $$
其中,$\small {v = 50η\mathrm {Hz}}$,$\small {L_0 = 1000η}$ 及 $\small {L_1 = 10000η}$,$\small {a_0 = 1-η}$ 及 $\small {a_1 = a_0 / 10}$,$\small {η} $ 是一个介于 0 和 1 之间的随机数,并且它等于 0 和 1 之间任何一个数的概率是一样的(可利用 MATLAB 的函数 rand 来实现)。用 $\small { F_s = 10000\mathrm {Hz}} $ 作为抽样频率,产生出 10 种不同情况下的接收信号,并将它们画在一起,从中观察多径效应和多普勒效应。对于这 10 种不同情况,求出结果信号并画出来。
答:
使用 MATLAB 模拟生成十种不同的接收信号:
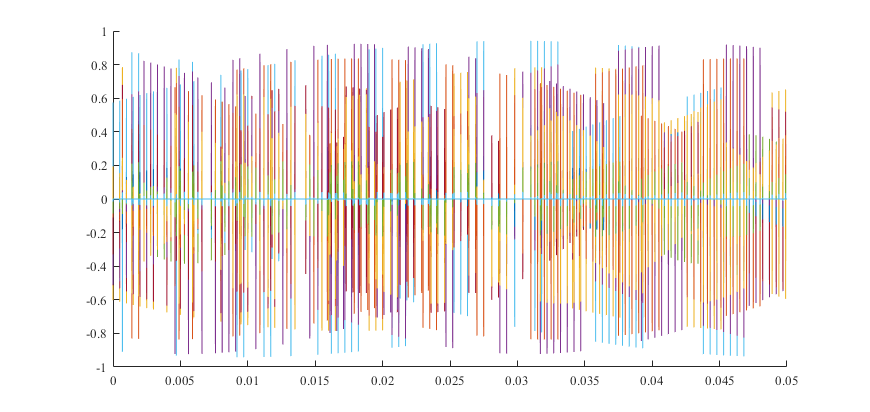
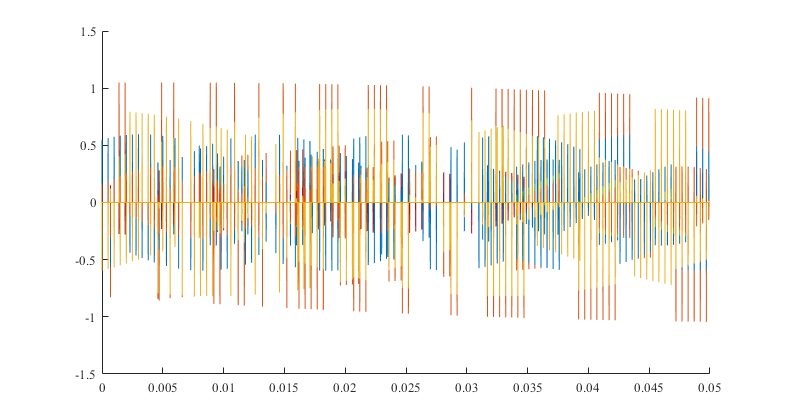
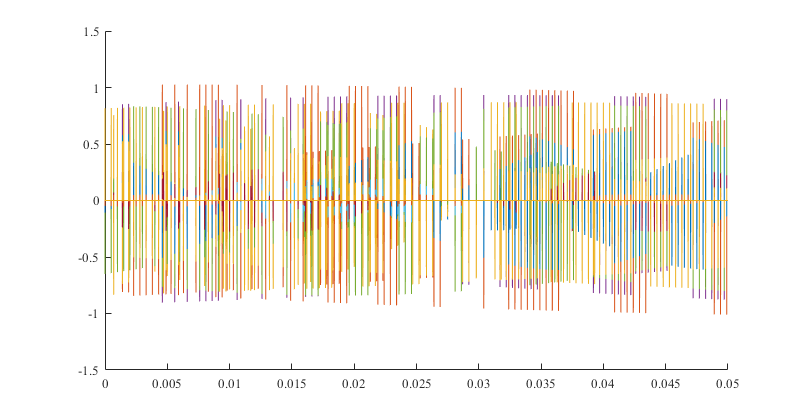
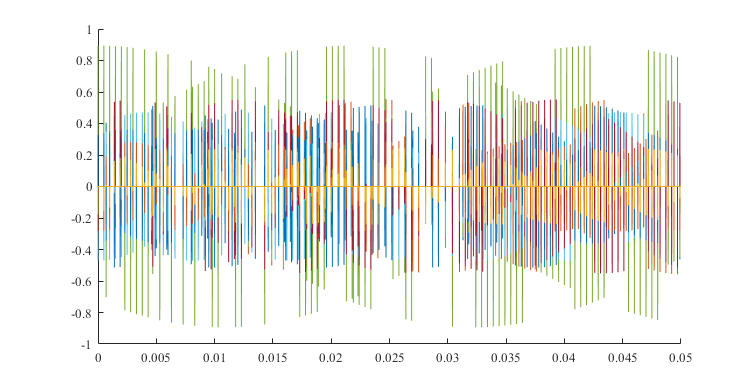
通过上述图形分析可以得出信号在传播过程中产生了明显的衰落,使结果信号的多径效应十分显著,许多信号的采样峰值都明显小于 1。信号在传播过程中产生了明显的频率变化,能够显著地观察到多普勒效应。其中多普勒效应最明显的信号甚至不能在图中完整地展示其一个周期。
三、参考文献
[1] 信号与线性系统分析,吴大正 杨林耀 张永瑞 王松林 郭宝龙,2019.3
[2] https://ww2.mathworks.cn/help/matlab/learn_matlab/help.html
四、附录
|
%f_0 = 7000Hz |
clc; clear |
clc; clear |




