OpenMMLab-1
初探深度学习与神经网络
一、计算机视觉四大基本任务
- 检测:如特定目标检测,通用目标检测等。
- 分割:如语义分割、实例分割、关键点检测等。
- 定位
- 分类
案例:虚拟主播,人脸识别,人体姿态跟踪等等。
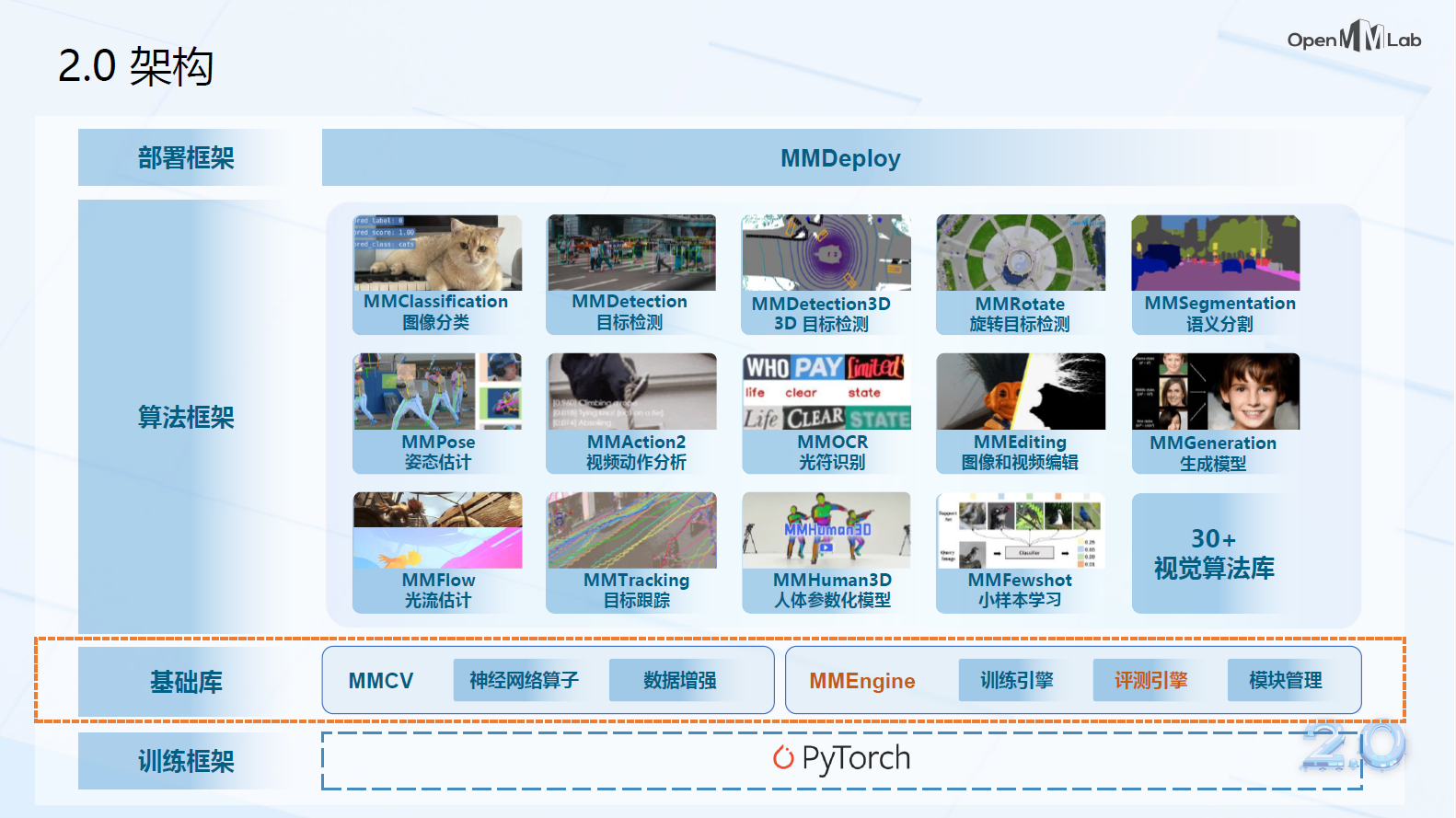
二、MMLab 算法框架
MMDetection:目标检测
MMClassification:图像分类
MMSegmentation:语义分割
MMPose &MMHuman3D:人体姿态
MMTracking:目标追踪
MMAction2:视频理解分析
MMOCR:文字检测
MMEditing:图像处理
……
三、机器学习
3.1 为什么要进行机器学习
从数据中学习经验,来解决特定问题
一般步骤:问题 —— 收集数据 —— 拟合模型
3.2 机器学习的典型范式
1、监督学习:数据之间存在某种映射关系,如何基于有限的数据样本推断出这种关系?
2、无监督学习:数据自身是否存在某种 “结构或 " 规律”?
3、强化学习:如何和环境交互,以获得最大收益?
3.3 机器学习的基本流程
1、训练:采集一些数据,标注它们的类别,从中选取一部分用于训练分类器,得到一个可以用于分类的分类器;
2、验证:从采集、标注的数据中另外选取一部分,测试所得分类器的分类精度。验证所用的数据不能和训练重合,以保证分类器的泛化性能:在一部分数据上训练的分类器可以在其余的数据上表现出足够的分类精度;
3、应用:将经过验证的分类器集成到实际的业务系统中,实现对应的功能。在应用阶段,分类器面对的数据都是在训练、验证阶段没有见过的。
3.4 机器学习中的分类问题
3.4.1 线性分类器
线性分类器假设类别和特征之间存在某种线性关系。针对某个样本 $\small {\left (x_1,x_2 \right)}$,计算 $\small {h\left (x_1,x_2 \right)}$ 的值:如果 $\small {h\left (x_1,x_2 \right) <0}$,归类为 A 类别;如果 $\small {h\left (x_1,x_2 \right)>0}$,归类为 B 类别。
更一般地,针对 $\small {d}$ 维特征向量 $\small { x\in \mathbb {R} ^d }$,线性分类器可以在数学上简写成向量内积的形式:
其中 $\small {w=\left (w_1,w_2,…,w_d \right)}$ 为分界面的法向量。一般利用感知器 Perceptron 来求解分界面,具体步骤如下:
1、随机初始化分类界面,记其法向量为 $\small {w}$;
2、依次检查每个样本 $\small {\left (x_i,y_i \right)}$,如果该样本被分类器分错,则把该样本累加到分界面的法向量上,即 $\small {w\gets w+\alpha x_iy_i}$,使其向正确的方向旋转一点。
3、可以证明,如果两类样本线性可分,算法最终会找到可以分开两类样本的分界面。
通常,称根据数据求解分类器参数的过程为训练或者学习。
3.4.2 非线性分类器
例如异或 (XOR) 是一个基本的布尔函数,是线性不可分的。但是异或函数可以用一个两层的计算图实现:第一层由 $\small {x}$ 输入到隐变量 $\small {h}$,第二层由 $\small {h}$ 输出到 $\small {y}$。
3.5 神经网络
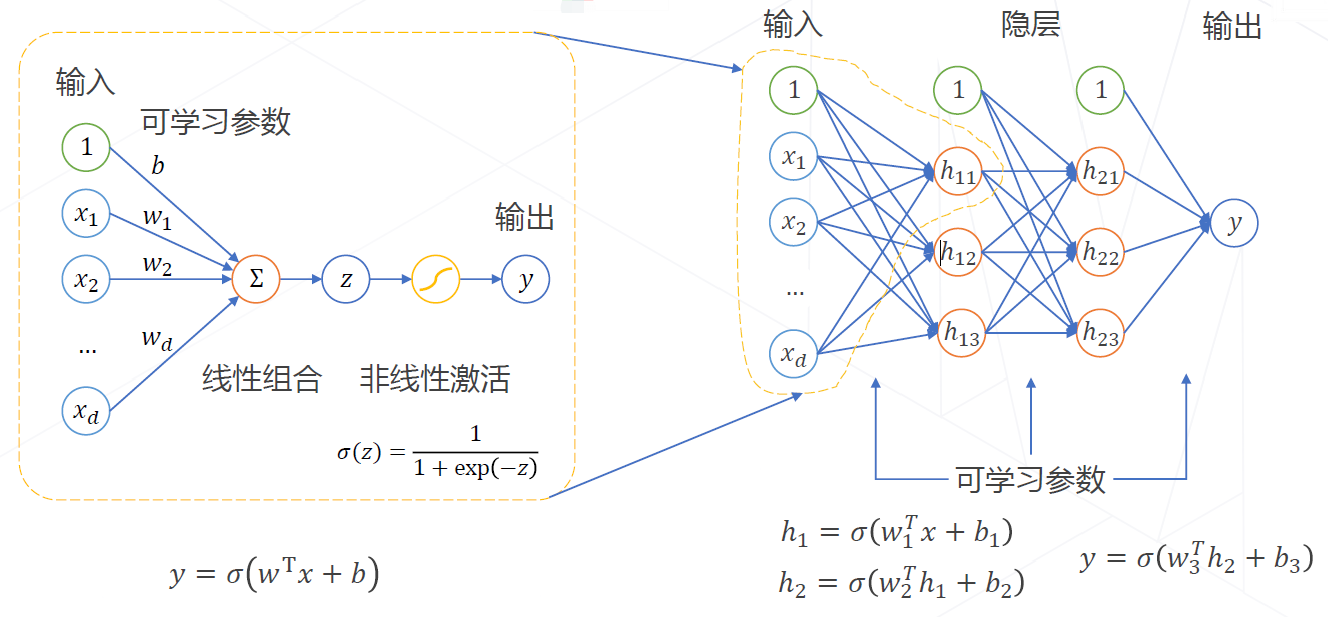
3.5.1 神经元
一些相关的术语解释:
1、权重 weight:不同的权值 $\small {w_i}$ 将会得到不同的输出结果。
2、偏置值 bias:输入数据进行加权求和之后,需要加上一个偏置值 $\small {b}$。
3、激活函数:给神经网络加入非线性变换 $\small {\sigma \left (z \right)}$,使其能够解决非线性分类问题。
4、多层感知器:单个神经元可以实现线性分类,而通过堆叠多层神经元可实现非线性分类。
5、多分类任务:如果是多分类任务,那么神经网络的输出就有多个结果 (多选一) $\small {y_1,y_2,y_3\cdots}$,每个输出 $\small {y_i}$ 介于 0~1 之间,且所有输出的和为 1,表示为一个有效的概率分布。为了满足多分类任务特性,输出层的激活函数使用 $\small {\mathrm {softmax}}$:
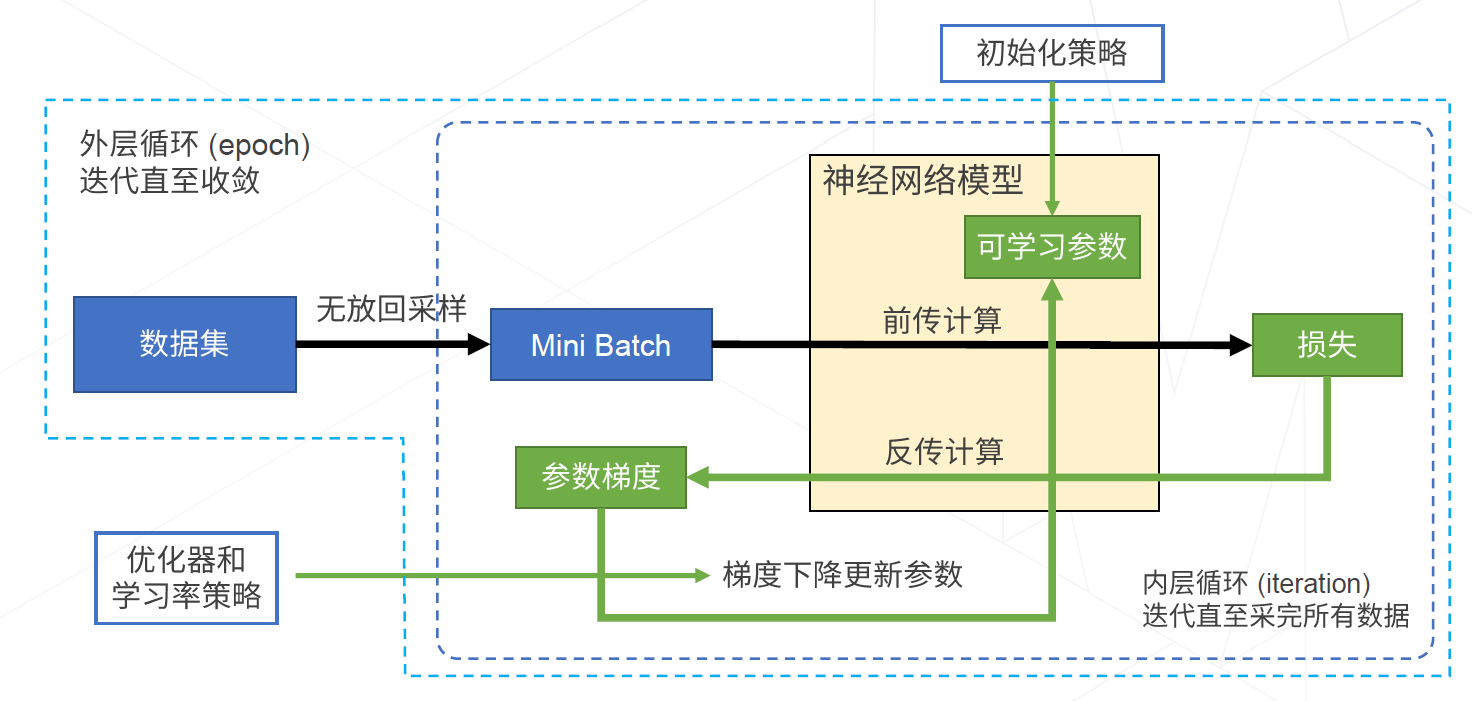
3.5.2 神经网络的训练
神经网络的训练流程:计算样本的损失 - 计算样本损失的梯度 - 据梯度信息更新参数
一些相关的术语解释:
-
1、损失函数:用于衡量神经网络的性能
神经网络的训练目标就是找到一组比较好的可学习参数 $w$ 的值,使得神经网络的性能最好。
从数学意义上讲,就是找到一组参数 $w$ 的值,使得损失函数 $L$ 的值最小。 -
2、梯度下降算法:寻找最优参数,进而得到最优网络
也就是寻找损失函数曲面的谷点。一般有标准梯度下降、随机梯度下降(SGD)、自适应梯度下降。
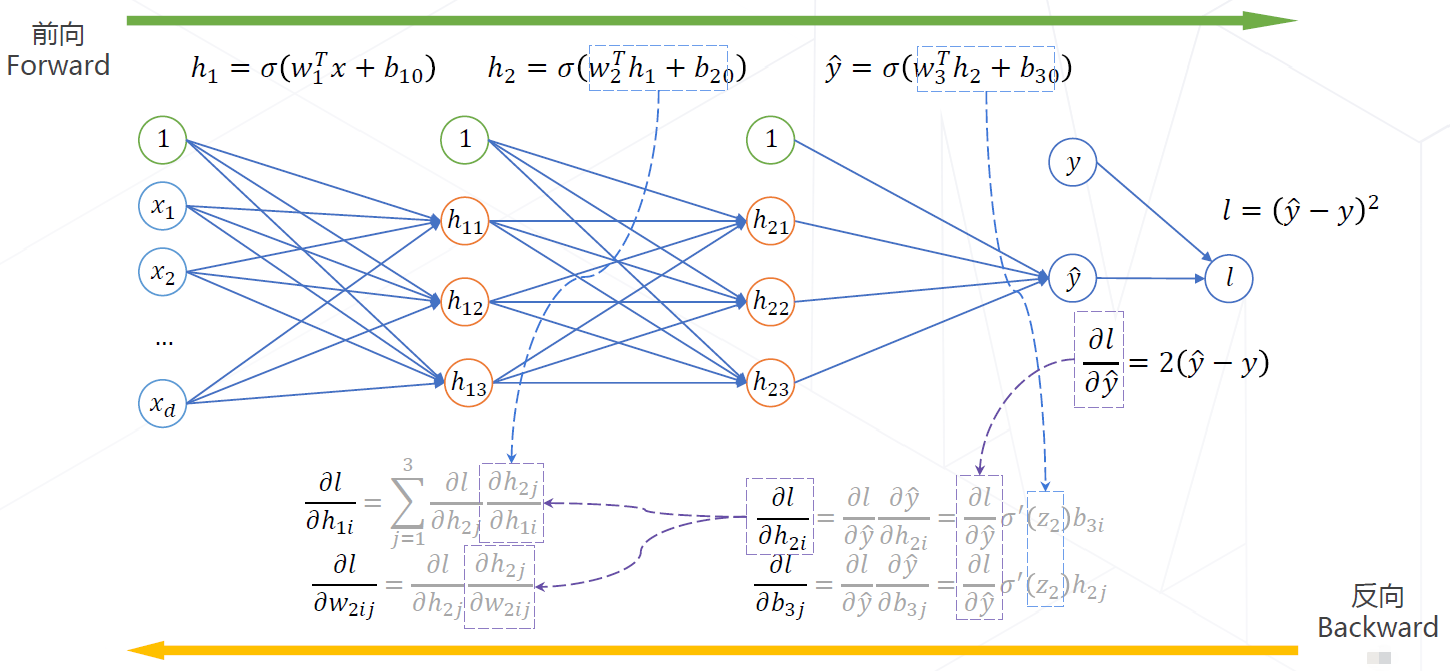
- 3、反向传播算法:计算损失函数 $\small {l}$ 对于所有隐层参数 $\small {\mathbf {\Theta}}$ 的梯度
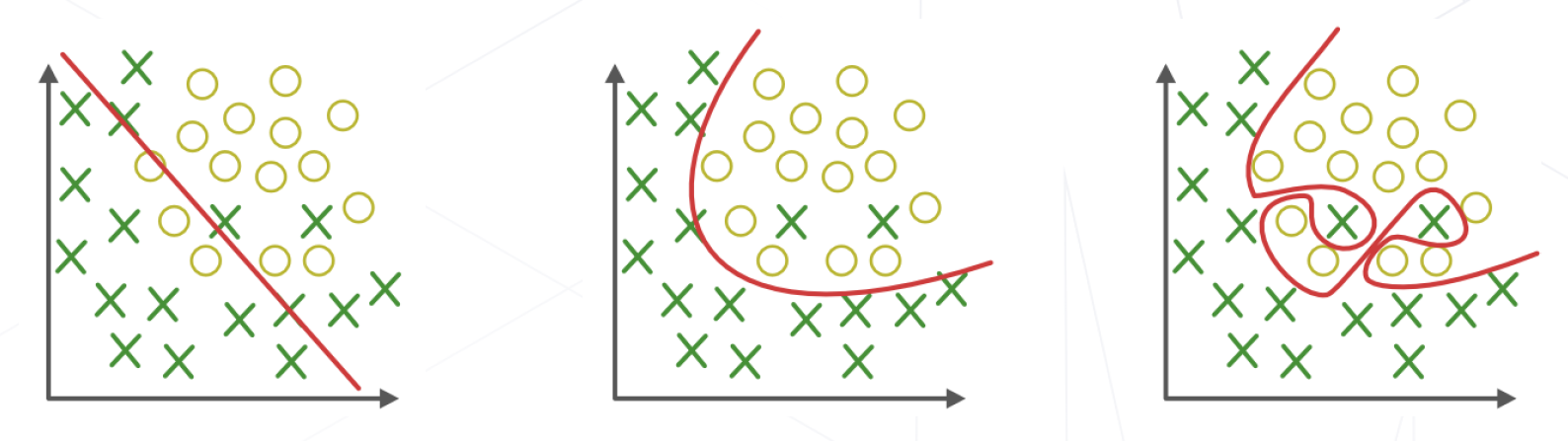
- 4、欠拟合、拟合与过拟合
欠拟合:
没有捕捉训练数据中的规律,不能准确预测未来 (测试集) 数据,模型过于简单。
拟合:
捕捉到训练数据中的规律,可以准确预测未来 (测试集) 数据。
过拟合:
过度拟合到训练数据中的噪声,不能准确预测未来 (测试集) 数据,模型过于复杂、且数据不够。
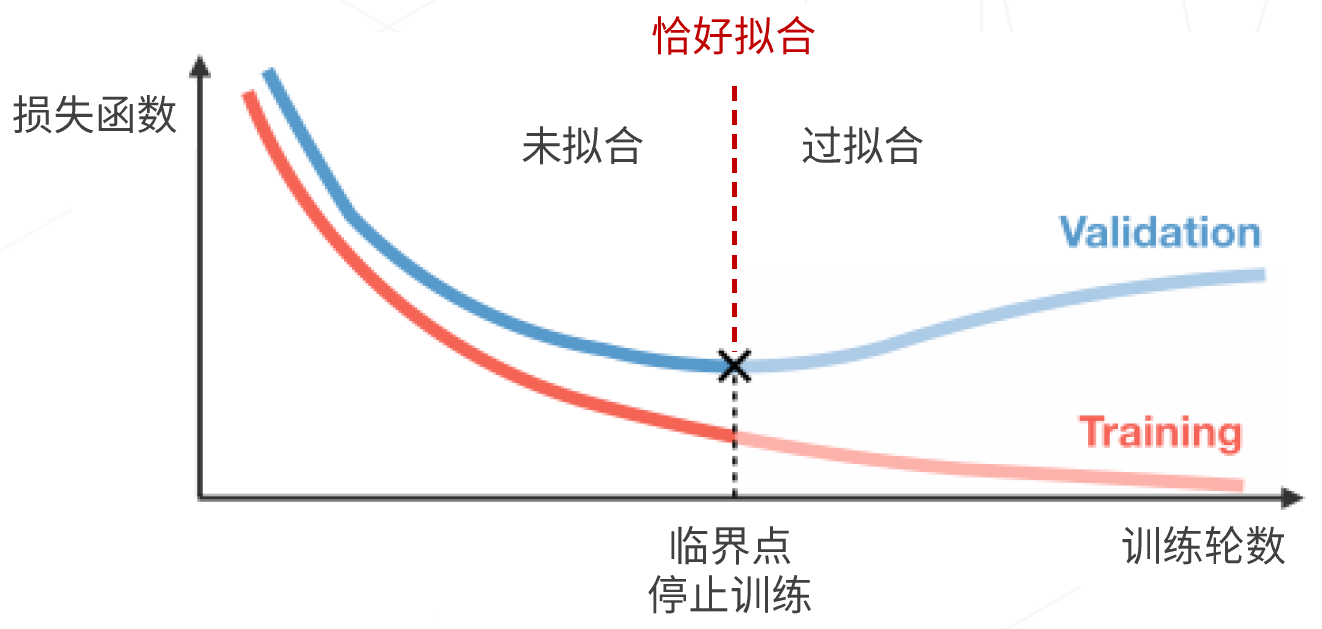
- 5、早停
将训练数据集划分为训练集和验证集,在训练集上训练,周期性在验证集上测试分类精度。当验证集的分类精度达到最值时,停止训练,防止过拟合。
3.5.3 卷积神经网络 (CNN)
特性:
1、局部连接:像素局部相关
2、共享权重:位移不变性
优点:大量节约参数,有效提取图像特征
流程结构:输入图像 - 卷积层 - 激活层 - 池化层 - 全连接层 - 概率输出 - 类别概率
四、几个热门 AI 研究方向
- 人工智能的可解释性分析、显著性分析
- 图机器学习、图神经网络 (AlphaFold2)、知识图谱
- 人工智能 + VR/AR/数字人/元宇宙
- 轻量化压缩部署 : Web 前端、智能手机、服务器、嵌入式硬件
- Al4Science:天文、物理、蛋白质预测、药物设计、数学证明
- 做各行各业垂直细分领域的人工智能应用
- 神经辐射场 (NERF)
- 扩散生成模型 (Diffusion)、AIGC、跨模态预训练大模型
- 隐私计算、联邦学习、可信计算
- AI 基础设施平台 (数据、算力、教学、开源、算法工具包)
- 认知科学 + 类脑计算 + 计算神经科学






